«Este es un artículo sobre los aspectos matemáticos de la epidemia COVID-19 en Chile, orientado a un público general, no solo especialistas. Explicaremos cómo los científicos logramos predecir el avance de la epidemia usando modelos matemáticos (…)» Así comienza el artículo Evolución de las epidemias: la matemática de aislarse del PhD en Ciencias de la Complejidad Social, Jorge Castillo, realizado junto al PhD en Matemática, Héctor Pastén, quienes aseguran que “explica de manera muy coloquial cómo una epidemia va creciendo en el tiempo, desde lo más sencillo, hasta un modelo un poco más sotisficado, al que se llamamos «SIR simplificado», que modela la cantidad de Susceptibles, Retirados e Infectados, sin la necesidad del uso de ecuaciones diferenciales”.

Desde el primer caso de COVID-19 detectado en nuestro país el 3 de marzo, el aumento (prácticamente) exponencial que se ha evidenciado hasta hoy, es alarmante. El número de contagiados sobrepasa los 4 mil a la fecha y es, en este escenario, en donde los investigadores Castillo y Pastén, buscan “crear conciencia sobre la importancia del aislamiento como medida para frenar el crecimiento del COVID-19 en Chile, y entregar herramientas educativas sobre cómo los científicos hacemos proyecciones en este tema”.

Así, utilizando un modelo matemático (*) en un lenguaje cercano y accesible, los científicos intentan predecir el avance de una epidemia que, en este caso, es el COVID-19. El modelo inicial que usan para su artículo es el exponencial: en un período de tiempo determinado, la cantidad de contagiados se va multiplicando por una constante fija. Esto es para entender la fase inicial de una epidemia, pero hay que entender que no es un modelo tan preciso ya que no considera que solo los sanos pueden infectarse. Entonces, los investigadores proponen un modelo simple, pero inspirado en el modelo SIR clásico que se estudia en epidemiología (SIR: Susceptibles, Infectados y Retirados), con la salvedad de que es un modelo en variables discretas y que depende de una capacidad de contagio y de un factor de desfase. La ventaja de este modelo, además de poder explicado con matemática del colegio, sin usar ecuaciones diferenciales, es que se necesitan unos pocos datos en la fase exponencial para determinar los parámetros, y es robusto frente al parámetro de desfase, cuestión que demuestran al final en un lenguaje un poco más técnico. Si bien es de carácter predictivo, los autores aseguran que “los modelos matemáticos bien diseñados y que toman en cuenta sus falencias al analizar una predicción, son una valiosa herramienta en la toma de decisiones”.

Desglose

La Sección 1 contiene “algo” de matemática (“¡muy sencilla!”, en palabras de los propios científicos), y 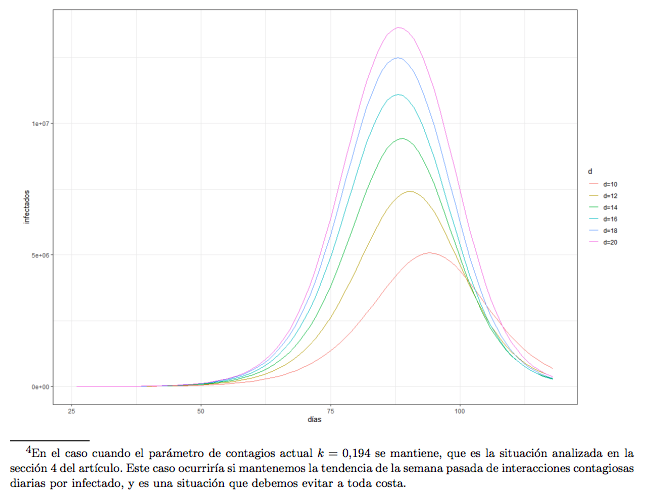leerla “es un ejercicio que, por responsabilidad, debería hacer”. Se presenta el método más sencillo de proyectar el avance de la epidemia con algunas proyecciones de lo que podría venir para Chile en abril.

La Sección 2 contiene una versión más refinada del análisis elemental de la Sección 1. Aquí se presenta el modelo exponencial de crecimiento de epidemias. La evidencia indica que actualmente el ritmo de contagio es cercano a un caso nuevo al día por cada 5 contagiados.

La sección 3 presenta el modelo SIR y una versión simplificada del mismo. Este modelo para predecir el comportamiento de epidemias es más realista y, por tanto, da predicciones más confiables a mayor plazo que el modelo exponencial.

La sección 4 usa datos reales en el modelo SIR simplificado para predecir cómo evolucionará el COVID-19 en Chile si continuamos al mismo ritmo que hasta ahora. A este ritmo, la predicción es un primer peak de la enfermedad entre fines de Mayo y comienzos de Junio. El número de casos se saldría de control mucho antes. Además, se explica por qué modelos como el SIR tienen crecimiento exponencial en etapas iniciales.

La Sección 5 examina las proyecciones si se baja la frecuencia de contagios con una estrategia drástica de aislamiento. Esto supone una acción inmediata: cada día se empeora críticamente la situación debido a que, en esta etapa temprana de la epidemia, el modelo de crecimiento exponencial todavía es válido.

Sobre los autores

Jorge Castillo Sepúlveda, es ingeniero civil matemático de la Universidad de Concepción y Doctor en Ciencias de la Complejidad Social (2019) de la Universidad del Desarrollo. Actualmente se desempeña como científico de datos en Z Data Lab, donde lidera las áreas de inteligencia de precios e inteligencia comercial, y es investigador en la Universidad del Desarrollo, donde realiza labores en proyectos asociados al tratamiento de datos y en docencia de posgrado.

Héctor Pastén Vásquez es un matemático de la Pontificia Universidad Católica de Chile. Doctor en Matemáticas de la Universidad de Concepción y Doctor en Matemáticas de la Queen’s University (2014). Anteriormente, fue investigador en la Universidad de Harvard (2014- 2018) y en el Institute for Advanced Study de Princeton (2015-2016). Ganador de la Medalla de Oro al Mérito Académico del Gobernador General de Canadá (2014) y del premio MCA del Mathematical Council of the Americas (2017) entre otros galardones internacionales.

(*) Un modelo matemático es una forma de utilizar las matemáticas para tratar de predecir el futuro a partir de datos conocidos.